W - Algorithms
All points are compared in a pairwise way and a coefficient of correlation (Pearson) is computed between the two series under comparison.
The coefficient of correlation is then transformed into a local similarity coefficient.
In the current version of the unique algorithm available, neither alignment nor stretching is performed.
It means that data should be aligned and monotonous.
Comparison logic:
--- spectrum comparison ---
'''W_ByIndex
'''Compare srce.m_Values[i].Y with ref.m_Values[i].Y
'''The number of values in each field should be the same
'''For each index, the distance between the source (s) and reference (r) is given by: abs(s - r) / max(abs(s), abs(r))
'''W_Interpolate
'''Compare the Y values from the source spectrum with the reference spectrum
'''For each srce.m_Values[i].X and ref.m_Values[i].X, the corresponding reference or source Y value is interpolated.
'''The distance between the source (s) and reference (r) values is given by: fabs(s - r) / max(fabs(s), fabs(r))
'''Optimistic means that values that cannot be interpolated are simply ignored. Only the range of values existing in both waves are taken into account.
W_Correlation
Compare the Y values from the source spectrum with the reference spectrum
For each srce.m_Values[i].X and ref.m_Values[i].X, the corresponding reference or source Y value is interpolated.
The source and the reference interpolated values are used to compute the Pearson correlation coefficient.
--- W peaks comparisons ---
W_sym
Scan the source and the reference values and increase the similarity every time a source value is in the range [ref.x - tolerance, ref.x + tolerance]
The final similarity = sum of the similar lanes / (source lane n° + ref lane n° - similar lane n°)
W_sympro
Scan the source and the reference values and increase the similarity every time a source value is in the range [ref.x * (1.0 - tolerance), ref.x *(1.0 + tolerance)]
The final similarity = sum of the similar lanes / (source lane n° + ref lane n° - similar lane n°)
W_id
Scan the source and the reference values and increase the similarity every time a source value is in the range [ref.x - tolerance, ref.x + tolerance]
The final similarity = sum of the similar lanes / source lane n°
W_idpro
Scan the source and the reference values and increase the similarity every time a source value is in the range [ref.x * (1.0 - tolerance), ref.x *(1.0 + tolerance)]
The final similarity = sum of the similar lanes / source lane n°
W_close
Divide the distance to the closest p_Ref band by the greatest of the two bands
At the end, sum all best links and divide by the number of comparisons (= the number of m_Values[i])
W_pearson
The correlation coefficient:
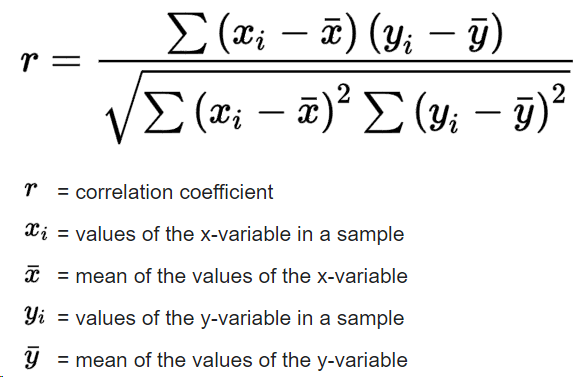
the final similarity is: sim = max_(0.0, r)
W_pearson_reverse
idem. The final similarity is: sim = max_(0.0, -r)
W_closesym
Identical to the Close algorithm, but commutative: sim = (sim(srce, ref) + sim(ref, srce)) / 2.0
W_neili
// Distance equation: Dxy = 2 * Nxy / (Nx + Ny) where:
Nxy is the number of shared lanes between the source and the reference,
Nx is the number of source lanes,
Ny is the number of reference lanes.
example 1 : Source 1010100011
Reference 1010111100
Nx = 5
Ny = 6
Nxy = 3
Dxy = 2 * 3 / (5 + 6) = 0.5455
example 2 : Source 1110011000
Reference 1110000001
Nx = 5
Ny = 4
Nxy = 3
Dxy = 2 * 3 / (5 + 4) = 0.6666
As we compare double values instead of binary values, we use the tolerance to known if the source and the reference are similar, as in the SYM algorithm.

