BioloMICS menu

S - Algorithms

S characters can be handled by several algorithms: SPOA, SPOS, SPPA, SPPS, SMD:

SPOA (Size Positional Asymmetric algorithm)

This algorithm was originally designed for the identification purpose.

Let’s call the unknown OTU1 and the known one OTU2.

Although for both OTU1 and OTU2 minimum (SM), lower percentile (SL), higher percentile (SH) and maximum (SS) have been recorded, one will only use SM and SS for OTU1 but SM, SL, SH and SS will be used for OTU2.

Comparisons are performed in 3 steps:

In the first step, SMOTU1 is compared with the values of OTU2. A first similarity coefficient SInf will be calculated.

If SLOTU2 <= SMOTU1 <= SHOTU2 then SInf = 1 (see green arrow in figure below).

If SMOTU2 <= SMOTU1 < SLOTU2 then SInf = 1 (see yellow arrow in figure below).

If SHOTU2 < SMOTU1 <= SSOTU2 then SInf = 1.

In the orange areas (tolerance (Z) that can be defined and changed by the user; see orange arrow in figure below), the SInf is inversely proportional to the distance between SMOTU1 and SMOTU2 (lower part) or SSOTU2 (higher part).

With the SPOA algorithm, the amplitude (A) of the lower and higher tolerance are not the same but are a percentage of SMOTU2 and SSOTU2 respectively. So if Z = 0.2 and if SMOTU1 = 3 then the amplitude of the lower tolerance is 0.2*3 (A=0.6), which means that in the region between 2.4 (=3-[0.2*3]) and 3, the similarity will gradually decrease. The same computation will be done in the higher part of the range of OTU2.

If (SMOTU2 -A) <= SMOTU1 < SMOTU2 then SInf = 1-(SMOTU2-SMOTU1)/SMOTU2

where, A = Z * SMOTU2

If (SSOTU2 +A) => SMOTU1 > SSOTU2 then SInf = 1+(SSOTU2-SMOTU1)/SSOTU2

where, A = Z * SSOTU2

If (SMOTU2 -A) > SMOTU1 then SInf = 0

where, A = Z * SMOTU2

If (SSOTU2 +A) < SMOTU1 then SInf = 0

where, A = Z * SSOTU2

Some special cases with decimal and null values are also handled in a particular way but are not explained here.
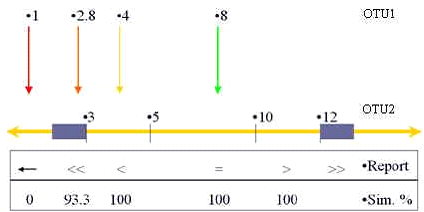
In the second step, the SSup is calculated using the exact same principles and formulas seen above. So in all formulas, SMOTU1 should be replaced by SSOTU1.
In the last step, the Sm is calculated as the average between SInf and SSup.

Therefore, Sm = (SInf + SSup) / 2

In the other special case where SMOTU1 < SMOTU2 and SSOTU1 > SSOTU2 then Sm will not be calculated and the character will not be accounted. This was decided since SPOA, is an algorithm that should be used in identification. Because of this, the fact that the unknown has a (much) larger range than the reference (here OTU2) may mean that the variability of OTU2 (usually a reference) has not been well observed.

The SPOA and SPOS algorithms are certainly the most suitable algorithms to handle continuous data in the identification processes. Unique, single values can be as well handled as range values. Also with, the use of the tolerance*, values that are very close but nevertheless different may not abruptly be considered equal to 0. This leads to similarity coefficients that are higher than with other algorithms like SPPA, SPPS or even possibly SMD. Both algorithms (SPOA and SPOS) produce comparisons that are not symmetrical (Sab=Sba), not necessarily transitive and not suitable for classification purpose.

*The less reliable the data (of a character in a given database), the larger the tolerance should be.

SPOS (Size Positional Symmetric algorithm)

This algorithm was originally designed for the identification purpose.

Let’s call the unknown OTU1 and the known one OTU2.

Comparisons are performed in 3 steps:

In the first step, SMOTU1 is compared with the values of OTU2. A first similarity coefficient SInf will be calculated.

If SLOTU2 <= SMOTU1 <= SHOTU2 then SInf = 1 (see green arrow in figure below).

If SMOTU2 <= SMOTU1 < SLOTU2 then SInf = 1 (see yellow arrow in figure below).

If SHOTU2 < SMOTU1 <= SSOTU2 then SInf = 1

In the orange areas (tolerance (Z) that can be defined and changed by the user; see orange arrow in figure below), the SInf is inversely proportional to the distance between SMOTU1 and SMOTU2 (lower part) or SSOTU2 (higher part). With the SPOS algorithm, the amplitude (A) of the lower and higher tolerance are the same and are equal to Z. So if Z = 2 and if SMOTU1 = 3 then the amplitude of the lower tolerance is also 2, which means that in the region between 1 (=3-2) and 3, the similarity will gradually decrease. The same computation will be done in the higher part of the range of OTU2.

If (SMOTU2 -A) <= SMOTU1 < SMOTU2 then SInf = 1-(SMOTU2-SMOTU1)/Z

If (SSOTU2 +A) => SMOTU1 > SSOTU2 then SInf = 1+(SSOTU2-SMOTU1)/Z

If (SMOTU2 -A) > SMOTU1 then SInf = 0

If (SSOTU2 +A) < SMOTU1 then SInf = 0

Some special cases with decimal and null values are also handled in a particular way but are not explained here.
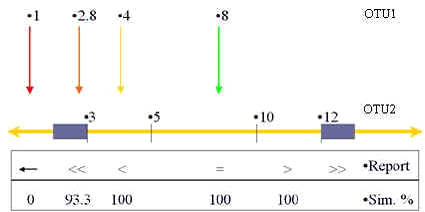
In the second, the SSup is calculated using the exact same principles and formulas seen above. So in all formulas, SMOTU1 should be replaced by SSOTU1.
In the last step, the Sm is calculated as the average between SInf and SSup.

Therefore, Sm = (SInf + SSup) / 2

In the other special case where SMOTU1 < SMOTU2 and SSOTU1 > SSOTU2 then Sm will not be calculated and the character will not be accounted. This was decided since SPOS, is an algorithm that should be used in identification. Because of this, the fact that the unknown has a (much) larger range than the reference (here OTU2) may mean that the variability of OTU2 (usually a reference) has not been well observed. So, in the report, '' will be printed, but not similarity will be produced.

The SPOA and SPOS algorithms are certainly the most suitable algorithms to handle continuous data in the identification processes. Unique, single values can be as well handled as range values. Also with, the use of the tolerance*, values that are very close but nevertheless different may not abruptly be considered equal to 0. This leads to similarity coefficients that are higher than with other algorithms like SPPA, SPPS or even possibly SMD. Both algorithms (SPOA and SPOS) produce comparisons that are not symmetrical (Sab=Sba), not necessarily transitive and not suitable for classification purpose.

*The less reliable the data (of a character in a given database), the larger the tolerance should be.

SPPA (Size superPosition Asymmetric algorithm)

The idea of the SPPA algorithm is to find the common portion of the range of the two OTU's under comparison.

Let’s call the unknown OTU1 and the known one OTU2.

Although for both OTU1 and OTU2 minimum (SM), lower percentile (SL), higher percentile (SH) and maximum (SS) have been recorded, one will only use SM and SS. With SPPA, the portion of the range shared by both OTU's is divided by the range of the OTU to be identified or the unknown or the first element of the comparison (OTU1).

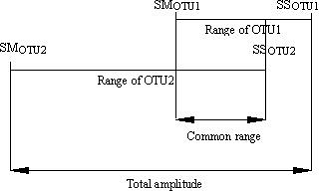
If SSOTU1 - SMOTU1 ¹ 0 then Sm = RC/(SSOTU1 - SMOTU1)

Where, RC is the range in common

If SSOTU1 - SMOTU1 = 0 then if SMOTU2 <= SMOTU1 <= SSOTU1 then Sm = 1

else SInf = 0

The SPPA algorithm is not using the tolerance concept. Therefore, its use may result in similarity coefficients that may be lower than SPOA, SPOS or even SMDA. Also, SPPA will lead to more abrupt decisions since even if two OTU's are very close, if they don't share the same range then the similarity will be null. This algorithm is suitable in the identification processes for characters where the range (of the reference OTU or the second element of the comparison - here OTU2) was well established and not null. SPPA produces comparisons that are not symmetrical (Sab=Sba), not necessarily transitive and not suitable for classification purpose.

SPPS (Size superPosition Symmetric algorithm)

The idea of the SPPA algorithm is to find the common portion of the range of the two OTU's under comparison. Let’s call the unknown OTU1 and the known one OTU2. Although for both OTU1 and OTU2 minimum (SM), lower percentile (SL), higher percentile (SH) and maximum (SS) have been recorded, one will only use SM and SS. With SPPA, the portion of the range shared by both OTU's is divided by the range of the OTU to be identified or the unknown or the first element of the comparison (OTU1).

TA = total amplitude

If TA ≠ 0 then Sm = RC / TA where, RC is the range in common

If TA = 0 then if SMOTU2 = SMOTU1 then Sm = 1

else SInf = 0

In the report file, all Sm of all pairwise comparisons will be displayed.

The SPPS algorithm is not using the tolerance concept. Therefore, its use may result in similarity coefficients that may be lower than SPOA, SPOS, SPPA or even SMDA. Also, SPPS will lead to more abrupt decisions since even if two OTU's are very close, if they don't share the same range then the similarity will be null. This algorithm is suitable in the identification and classification processes for characters where the range was well established. SPPS produces comparisons that are symmetrical (Sab=Sba), but not necessarily transitive. It's a good algorithm for classification purpose.

SMD (Size Median algorithm)

The idea of the SMD algorithm is to calculate the distance between the two medians or mid-range values of the OTU's under comparison.

Let’s call the unknown, OTU1 and the known one, OTU2.

Although for both OTU1 and OTU2 minimum (SM), lower percentile (SL), higher percentile (SH) and maximum (SS) have been recorded, one will only use SM and SS.

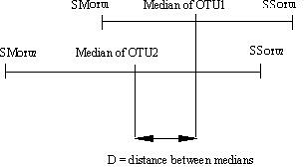
if Med1 = Median of OTU1 and Med2 = median of OTU2

D = | Med1 – Med2 |

If Med1 < Med2

then Sm = 1 – D / Med2

If Med1 > Med2

then Sm = 1 – D / Med1

If (Med1 = 0 or Med2 = 0) : Sm = 1 if Med1 = Med2 and 0 otherwise

If the median is null then it is assumed that the characters is absent.

The SMD algorithm is not using the tolerance concept. SMD will produce similarity coefficient that are rarely null and rarely equal to 1. Except to compute the median values, ranges of the OTU's under comparison are not accounted. Two very different ranges may result in the same median value. Therefore this algorithm should preferably be used when the range values are not really well established or when single values are encoded (range is null). This algorithm is suitable in the identification and classification processes. SMD produces comparisons that are symmetrical (Sab=Sba), but not necessarily transitive.